前言
机器学习,神经网络,已经不算前言的名词、未来的趋势。未来大部分的工作都可能会被机器所取代,这不是危言耸听。秉承着不能被机器淘汰的思想,必须了解到机器到底在学习什么,怎么能学习。本系列文算是个人对机器学习的一个笔记,加上自己的一些总结和变化。记录的过程即是加深学习的过程,希望可以今年内将这个系列学习完,也希望对访问博客的朋友们有所帮助。本文大部分内容引用、整理或翻译自Michael Nielsen的《Neural Networks and Deep Learning 》,已征得原作者许可,转载此文请先与我联系。作者原声明如下:
This work is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. This means you’re free to copy, share, and build on this book, but not to sell it. If you’re interested in
commercial use, please contact me.

本文主要内容包含:
- 神经网络: 一个从生物学得到启发的漂亮的编程方法,让电脑可以从可观察的数据中进行学习
- 深度学习:运用神经网络机型学习的极为有效的技术体系
概念
神经网络和深度学习在处理图像识别、音频识别以及自然语言处理问题时能提供最佳的解决方案。 例如:人类可以很轻易地识别如下手写数字序列(基本上算是很直觉地识别出)。但是对计算机来讲,却是很复杂的事情,且无法运用人类的识别方式。
Fig 1. 手写字体
一般来说计算机识别步骤为:
- 准备一系列已知的手写数据范例(如下图),称为训练数据
- 创造一个识别系统,从这些手写数据范例中归纳出识别的模式。

Fig 2. 手写字体范例
感知器
感知器是神经网络的基本结构,而神经网络正是参照了人类神经系统的特性构造起来的,其基本单元为_感知器_。要了解感知器,先看一张人类神经元的结构图。

Fig 3. 神经元
神经元的解释如下(来自百度百科):
神经细胞是神经系统最基本的结构和功能单位。分为细胞体和突起两部分。细胞体由细胞核、细胞膜、细胞质组成,具有联络和整合输入信息并传出信息的作用。突起有树突和轴突两种。树突短而分枝多,直接由细胞体扩张突出,形成树枝状,其作用是接受其他神经元轴突传来的冲动并传给细胞体。轴突长而分枝少,为粗细均匀的细长突起,常起于轴丘,其作用是接受外来刺激,再由细胞体传出。
可见,其主要作用就是接受其他神经元的刺激,并传导到其他神经元。可以理解为神经元为多输入输出的一个基本单元。神经网络中的感知器工作原理也类同,如下图:它接受其他感知器的输出作为输入,乘上一定的权值加总后得到一个值。用函数$$f$$对该加总值进行处理,得到输出$$O$$。这个输出值是一个二元值,0或1,类比表示神经元是否产生输出刺激。公式如下:
$$ \begin{eqnarray} \mbox{output} & = & \left\{ \begin{array}{ll} 0 & \mbox{if } \sum_j w_j x_j \leq \mbox{ threshold} \\ 1 & \mbox{if } \sum_j w_j x_j > \mbox{ threshold} \end{array} \right. \tag{1}\end{eqnarray} $$
令 $$ b = \mbox{-threshold} $$,即有:
$$ \begin{eqnarray} \mbox{output} & = & \left\{ \begin{array}{ll} 0 & \mbox{if } \sum_j w_j x_j +b\leq \mbox{0} \\ 1 & \mbox{if } \sum_j w_j x_j+b > \mbox{ 0} \end{array} \right. \tag{2}\end{eqnarray} $$
如何理解上述公式?通常人类要做一件事情的时候,一定会有很多条件的输入。每个条件都有一定的优先级,综合考虑每个条件之后,做出最后的判断。例如:老王想要决定晚上出不出去健身,影响他判断的条件可能有晚上会不会加班、今天天冷不冷、昨天有没有建过身等。
在机器学习中,这些输入条件即可用$$x_1$$到$$x_i$$表示,而每个条件对做出最后决策的影响成都即 $$w_1$$到$$w_i$$ 。这些数据的加总和通常不会是1或者0这样的结果,因此无法直接用来判断输出的结果。通常,上述公式感知器会将该加总和与阈值threshold进行比较。如果大于阈值则输出1,反之则输出0。

Fig 4. Perceptron(感知器)
神经网络
神经网络即由上述感知器作为神经元的网络(如Fig 5)。其基本组成为:
- 感知器:即下图每一个小圆,神经网络的“神经元”
- 输入层:由N个感知器组成的层次(N为输入条件的个数)
- 输出层:有M个感知器组成的层次,(N为机器学习问题输出值的个数。对手写数字识别来讲,即有10种可能输出,即输出层由10个感知器组成)
- 多个隐层(Hidden Layer): 非输入层也非输出层的中间层。可以为0个或者多个。
- 层与层连线上的参数 ,即感知器的权值 $$ w_{ij} $$ 和Threshold $$ b $$
输入层和输出层中感知器的数量、隐层及其所包含感知器的数量,取决于要解决的机器学习问题。往往这些数量以及 $$ w_{ij} $$ 等变量初始值的选择,也决定着机器学习的效率以及效果,之后会再探讨。

Fig 5. Neural Network(神经网络)
机器学习的过程,就是通过训练数据,反推出神经网络层与层之间所有的权值
$$ w_{ij} $$ 与阈值 $$ b $$ ,直到所有检验数据达到需要的精准度。
Sigmoid神经元
感知器一节提到的函数,只是简单地从输入端加权值减去阈值的结果来判断输出。
例,当_水温能达到28_度,今天就会出去游泳;又或,当_小黑心情不好时_,就睡觉。 这样的作法很直觉,也比较符合我们的思考习惯。这种函数,非0即1,不够平滑,函数输出值随着输入的跳变较大。如下图, 当$$ \sum_j w_j x_j +b\ $$超过0之后,输出就会直接跳变为1。这样造成的结果是,输入中的某一个权值轻微变化,造成输出结果发生剧变。

Fig 6. 函数(2)的图形
而机器学习的过程,希望的是输入值的变化对输出值的变化不要产生过大的变动。即上述函数的变化较为平滑。而Sigmoid函数正式这样的函数,它的公式如下:
$$f\equiv\frac{1}{1+e^{-{(W \bullet X-b)}}} \tag{3} $$
而该函数对应的几何图如下:

Fig 7. Sigmoid函数的图形
从图上可以看出,因为输出值为平滑的0到1曲线,不会出现因为 $$ \sum_j w_j x_j +b\ $$ 的变化出现明显的跳变(输入的较小改变,得到的也是最终输出结果较小的变化),是较为理想的感知器函数。其数学公式如下:
$$ \begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b, \tag{5} \end{eqnarray} $$
即,使用Sigmoid函数的导数是一个线性的函数,随着输入参数的变化,output的值是线性增长的。
有同学要问了,神经网络要解决的是一个是非题,但Sigmoid函数并非如此怎么办?
可以以0.5作为分界线,当Sigmoid的结果为0.5以上时,即认为最终的决策结果为“是”,反之为“否”
识别手写数字实战
带着前面神经网络的基础知识,再回来看开篇提到的课题:识别手写数字。再看下边这张图:
首先将问题分解:
- 将上述图片分割为6个独立的数字
- 对6个独立的数字分别进行识别

图片分解
问题一像是如何识别图片边界的问题,对计算机来讲也比较复杂。不过本文暂时先考虑如何编程来解决问题2。
为了解决这个问题,定义一个三层神经网络:输入层包含784个神经元;中间隐层包含15个神经元;而输出层则为10个神经元分别代表数字0~9。
- 输入层$$784=28*28$$,表示每个被分割出来的数字有28乘28个像素点组成。每个像素点值表示颜色深度:0值表示该像素位置为白色,1则表示黑色,0到1的中间数字表示介于黑白之间像素点的灰黑色深度。
- 隐层神经元个数的选择对学习效率是有影响的(事实上,如何选择这些初始值也是非常值得研究的课题)。本文从15作为初始选择,后边实例将会观察不同隐层神经元个数对学习结果的影响。
- 输出层则比较直觉,10个输出代表我们要识别的数字的10中可能。我们当然可以采用其他个数的神经元组合。例如:神经元代表每个二进制位的值,这样只需要4个神经元就能表示0
16的值。但事实上,这样的选择效果往往不会非常的理想。试想,110这10个数字的图片形状各不相同,如何用八个形状(4个bit*每个bit 2个值)来归纳这十个数字?
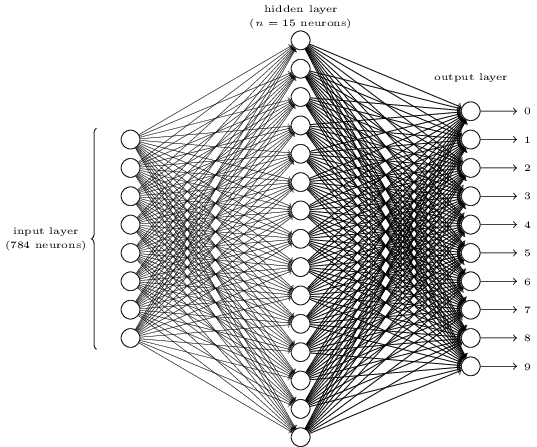
当然,本文采用的选择仅仅为一个启发而并非强制性的。或许有更好的参数,能进行更好更快的识别。
梯度下降法学习
前一节我们简单建立了用于学习的神经网络模型,接着需要有用于学习的数据集。MNIST收集了成千上万人的手写数字扫描数据,包含60000个训练数据以及10000个测试数据,均已被大小归一化乘28*28像素大小且居中对其。数据文件包括:
- train-images-idx3-ubyte: 训练集图片
- train-labels-idx1-ubyte: 训练集标签
- t10k-images-idx3-ubyte: 测试集图片
- t10k-labels-idx1-ubyte: 测试集标签
图片文件格式如下:
偏移
类型
数值
描述
0000
32位整形
0x00000803(2051
MAGIC Number(魔数)
0004
32位整形
60000 或 10000
图片个数
0008
32位整形
28
像素行数
0012
32位整形
28
像素列数
0016
无符号字节
?
像素点
0017
无符号字节
?
像素点
……..
无符号字节
?
像素点
xxxx
无符号字节
?
像素点
标签文件格式如下:
偏移
类型
数值
描述
0000
32位整形
0x00000801(2049
MAGIC Number(魔数)
0004
32位整形
60000
图片个数
0008
无符号字节
?
标签值(0-9)
0009
无符号字节
?
标签值(0-9)
……..
无符号字节
?
标签值(0-9)
xxxx
无符号字节
?
标签值(0-9)
本文使用$$x$$代表输入数据,它是一个28*28维向量。使用$$y=y(x)$$代表输出,其中$$y$$为10维向量。例,若输入图形$$x$$的输出结果为6,则用$$y(x)=(0,0,0,0,0,1,0,0,0,0)^T$$表示。
我们的目标就是找到所有权值及阈值,使得输出结果与所有的训练数据接近。我们可以定义如下误差函数:
$$\begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x \| y(x) - a\|^2 \nonumber\end{eqnarray}$$
$$w$$表示网络中的所有权重,$$b$$代表所有的阈值,$$n$$表示训练数据总量,$$a$$则是$$x$$作为训练数据时的输出结果向量。那么该误差函数$$C(w,b)$$表示的就是目标函数输出与实际训练数据结果的均方误差,mean squared error or just(MSE)。当目标函数与输出结果接近时,$$C(w,b) \approx 0$$。因此我们的目标便是对所有训练数据,使得目标函数结果与训练数据的输出接近(当然最好是相等,XD)。接下来就该梯度下降算法出场了。
介绍梯度下降算法前,先思考一个问题:为什么我们的误差函数是均方误差,而不使用训练数据正确的个数?会这样考虑的原因是:用数量作为误差函数,并非平滑函数。即,对权值或者阈值微小修改并不会对正确数量产生大的变化。这样的话很难对权重或者阈值修正来得到机器学习效果的提升。而如果我们采用较为平滑的误差函数,则能通过对权重或者阈值的变化得到提升。
这里又有疑问了:虽然是要用较平滑的函数作为误差函数,为什么一定要是均方误差函数?当然不必,之后文章会再研究是否有其他选择。但是对了解神经网络基础来讲,这个均方误差函数便已足够。
如前所述,我们训练的目标,是求出可以使得误差函数最小的所有的权值和阈值,而我们将会使用梯度下降算法。为了对这一算法进行阐述,我们先简化一下我们的问题:另我们的输入只有两个像素点,对应两个权值$$v_1和v_2$$,接着我们可以对应扩展到多个权值或阈值的场景。
如前所述,我们训练的目标,是求出可以使得误差函数最小的所有的权值和阈值,而我们将会使用梯度下降算法。为了对这一算法进行阐述,我们先简化一下我们的问题:另我们的输入只有两个像素点,对应两个权值$$v_1和v_2$$,接着我们可以对应扩展到多个权值或阈值的场景。
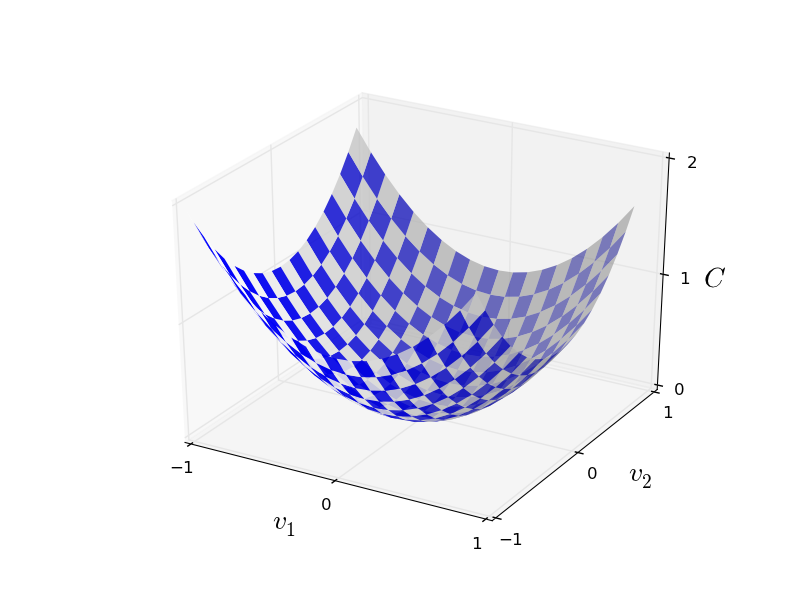
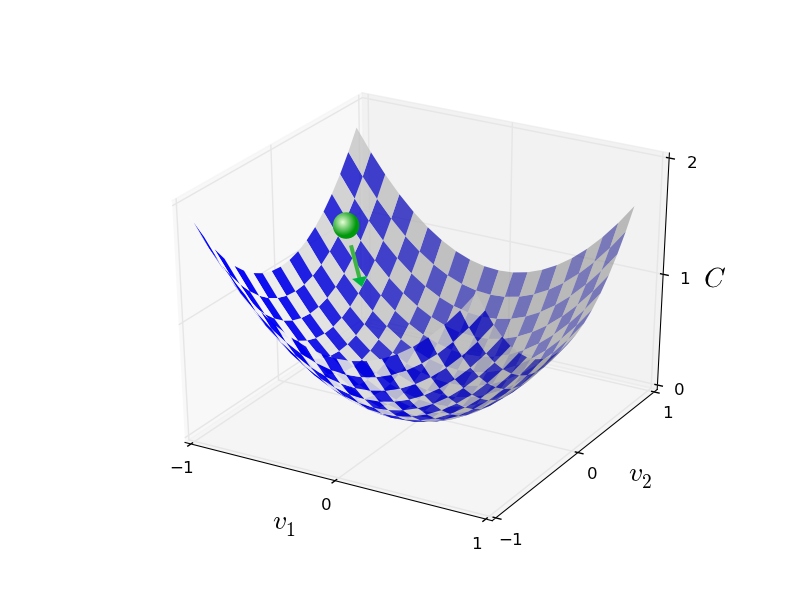
全局最小
对上图来讲,我们可以一眼大概看出C的全局最小的值,得到对应的$$v_1和v_2$$。但是事实上,C往往是一个复杂的函数包含了许多参数,也不可能一眼就看出其最小值。而解决此类问题(求C最小值)的一种分析方法就是微积分: 我们可以通过求导来找到使C达到最小的点。当C函数参数较少的时候,或许可以幸运地的找到。但是当参数更多时,这种方法便成了噩梦。不幸的是,往往我们的神经网络中有多得多的参数–最大的神经网络可能会有成千上万个权重和阈值要求出,是不可能用微积分得到最小值的。
不过不要担心,幸运的是我们可以用其他算法来做这件事并得到很好的效果。首先我们把误差函数的看作一个山谷(就如上图一样),想象有一个球从斜坡滚向山谷。根据日常经验,这个球最终会滚向谷底。那么或许我们可以用这种方法来找到函数的最小值?可以随机选择一个起始点,并模拟球向山谷滚动的运动。我们可以通过对C求导(或者有时是二次导数)来做这样的模拟,并得到“山谷的形状”,最终得到球该如何向下滚动。
请放心,我们这里不是讨论像牛顿定律这种物理。为了更准确地描述这个问题,假设这个球向$$v_1$$和 $$v_2$$ 放心分别移$$ \Delta v_1 $$ 和 $$ \Delta v_2$$ 。通过微积分我们可以得到:
$$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \tag{6}\end{eqnarray}$$
我们需要找到一种方式选择 $$\Delta v_1 和\Delta v_2 这样\Delta C $$是负值,即我们的球可以向谷底移动。我们首先定义向量 $$ \Delta v \equiv (\Delta v_1, \Delta v_2)^T $$ 来表示每个维度上的变化,其中T为矩阵转置。而C对每个变量偏导数组成向量,如下:
$$\begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T. \tag{7}\end{eqnarray} $$
其中 $$ \nabla $$ 符号表示梯度向量。公式(6)和(7)合并:
$$ \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v. \tag{8}\end{eqnarray} $$
通过以上公式,我们可以得到一种必定可以另 $$ \Delta C $$ 为负值的方法。选择
$$ \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{9}\end{eqnarray} $$
其中 $$ -\eta$$为一个比较小的正值,而根据公式(9)即知道 $$ \Delta C $$ 一定为负值或0。看起来我就可以用公式(9)来更新我们的参数,来保证我们的小球一定是向谷底移动的。即每次对参数做 $$ \Delta v = -\eta \nabla C $$ 大小的修正,最后得到全局最小(即我们的球也滚到了底部)。这样解释了算法的名称“梯度下降”。
简要说明梯度下降的思想后,我们如何将它用在神经网络中?注意到$$ v_1 和v_2$$ 是我们为了描述问题简化的,它们代表权值 $$ w_x 或者阈值 b$$ ,那么对公式(9)提到的 $$ v_1 和v_2$$ 更新方法,也同样适用在$$ w_x 或 b$$ ,即得到公式:
$$ \begin{eqnarray} w_k & \rightarrow & w_k’ = w_k-\eta \frac{\partial C}{\partial w_k} \tag{10}\\ b_l & \rightarrow & b_l’ = b_l-\eta \frac{\partial C}{\partial b_l}. \tag{11}\end{eqnarray} $$
对前文误差函数求偏导得到, $$ \nabla C = \frac{1}{n} \sum_x \nabla C_x $$,注意这里是对所有的训练数据做求偏导动作,当训练数据量很大时,学习时间会变得非常长。这时一种解决方案是,每次学习只取训练数据集的一部分m个,只要保证最后所有训练数据都有被取到且平均即可,那么公式为,
$$ \nabla C = \frac{1}{m} \sum_x \nabla C_x $$ 。最后我们得到参数的更新公式:
$$ \begin{eqnarray} w_k & \rightarrow & w_k’ = w_k-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{12}\\ b_l & \rightarrow & b_l’ = b_l-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l}, \tag{13}\end{eqnarray} $$
代码实例
介绍了这么多理论,还是直接看看代码吧。本文参考的原文使用numpy作为机器学习库。代码放在Github。
代码如下:
#### Libraries
# 标准随机库
import random
# numpy库
import numpy as np
class Network(object):
def __init__(self, sizes):
""“
sizes定义是每层神经网络的神经元(感知器)个数。例如若sizes=[2,3,1],那么它代表输入层2个感知器,隐层3个感知器,最后一层1个感知器。
"""
self.num_layers = len(sizes)
self.sizes = sizes
#初始化每层的权值w和b(bias即负的阈值)
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""返回感知器的输出z"""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""使用前文提到的‘每次学习只取训练数据集的一部分m个,只要保证最后所有训练数据都有被取到且平均即可’算法进行训练"""
if test_data: n_test = len(test_data)
n = len(training_data)
#训练轮数
for j in xrange(epochs):
#随机打乱训练数据
random.shuffle(training_data)
#根据训练最小包的个数分出多个训练包
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
#对每个训练数据包进行训练,权值w和b进行更新
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
#用测试数据对训练结果进行计算准确率
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""使用后传播方法对训练数据包进行训练(更新w和b)"""
#初始化所有的b和w
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
#根据包中所有的训练数据计算w和b要变化的幅度nabla_b和nabla_w
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
#根据计算的更新幅度更新w和b
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = []
# 根据w和b计算训练数据输入得到每个神经元输出
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# 计算输出层对w和b的偏导
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# 从倒数第二层到输入层计算每层w和b的更新值,这里的为BP神经网络算法的实现方法,后续会再介绍其原理。
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
#此处比较容易理解,使用测试数据和我们计算得到的w和b代入的公式得到结果对比计算当前学习的准确率
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
return (output_activations-y)#sigmoid函数
def sigmoid(z):
“””The sigmoid function.”””
return 1.0/(1.0+np.exp(-z))
#sigmoid函数的倒数
def sigmoid_prime(z):
“””Derivative of the sigmoid function.”””
return sigmoid(z)*(1-sigmoid(z))